New Model Supertype
Kirstine.jl comes with support for nonlinear regression models. The theory of optimal design is of course applicable also to other regression settings. This vignette explains how to extend Kirstine.jl so that we can also find optimal designs for logistic regression.
The statistical model is
\[\begin{align*} \Unit_{\IndexUnit} \mid π_{\IndexUnit} &\simiid \BernoulliDist(π_{\IndexUnit}) \\ \Logit(π_{\IndexUnit}) &= ν(\Covariate_{\IndexUnit}, \Parameter). \end{align*}\]
Since we allow the predictor to be a nonlinear function $ν : \CovariateSet × \ParameterSet → \Reals$, our setup is more general the usual logistic GLM where the predictor is linear.
Now, we need to find the Fisher information matrix of the model. With the log-likelihood
\[\LogLikelihood(\Unit,\Covariate,\Parameter) = \Unit \log(\Expit(ν(\Covariate, \Parameter))) + (1 - \Unit) \log(1 - \Expit(ν(\Covariate, \Parameter)))\]
and some calculations we arrive at
\[- \Expectation[\Hessian\LogLikelihood\mid\Parameter] = \Expit(ν) (1 - \Expit(ν)) \TotalDiff ν' \TotalDiff ν.\]
Implementation
First we introduce a new subtype of Kirstine.Model, and a corresponding ModelWorkspace to hold the preallocated Jacobian matrix of the predictor. Then we implement a method for average_fishermatrix! that specializes on logistic regression models and returns the upper triangle of the averaged Fisher matrices.
If we had any expressions that depend on $\Covariate$, but not on $\Parameter$, we could store them in additional fields of the ModelWorkspace and compute them in update_model_workspace.
using Kirstine, Plots, Random
import LinearAlgebra: BLAS
abstract type LogisticRegression <: Kirstine.Model end
# We can define this on the supertype since it will always be the case.
Kirstine.unit_length(m::LogisticRegression) = 1
struct LRWorkspace <: Kirstine.ModelWorkspace
jm_predictor::Matrix{Float64}
end
# We can ignore the number of design points `K` here.
function Kirstine.allocate_model_workspace(
K::Integer,
m::LogisticRegression,
pk::PriorSample,
)
return LRWorkspace(zeros(1, dimension(parameters(pk)[1])))
end
# nothing to do
function Kirstine.update_model_workspace!(
mw::LRWorkspace,
m::LogisticRegression,
c::AbstractVector{<:Kirstine.Covariate},
)
return mw
end
expit(x) = 1 / (1 + exp(-x))
function Kirstine.average_fishermatrix!(
afm::AbstractMatrix{<:Real},
mw::LRWorkspace,
w::AbstractVector,
m::LogisticRegression,
c::AbstractVector{<:Kirstine.Covariate},
p::Kirstine.Parameter,
)
fill!(afm, 0.0)
for k in 1:length(w)
# We need to implement the next two functions for concrete subtypes.
predictor_jacobianmatrix!(mw.jm_predictor, m, c[k], p)
prob = expit(nonlinear_predictor(m, c[k], p))
p1mp = prob * (1 - prob)
BLAS.syrk!('U', 'T', p1mp * w[k], mw.jm_predictor, 1.0, afm)
end
return afm
endThe call to BLAS.syrk! is a more efficient way to compute
afm .+= p1mp * w[k] * mw.jm_predictor' * mw.jm_predictorin-place. Since the result is symmetric, only the upper triangle of afm is filled.
Examples
Linear Predictor
We start with a linear predictor and a $c$-dimensional covariate
\[ν(\Covariate, \Parameter) = β₀ + \sum_{j=1}^c β_j x_j\]
where $\Parameter = (β_0, β_1, …, β_c)$.
struct LinLogReg <: LogisticRegression
dim_covariate::Int64
end
mutable struct LLRCovariate <: Kirstine.Covariate
x::Vector{Float64}
end
Kirstine.allocate_covariate(m::LinLogReg) = LLRCovariate(zeros(m.dim_covariate))
struct LLRParameter <: Kirstine.Parameter
beta_0::Float64
beta_rest::Vector{Float64}
end
Kirstine.dimension(p::LLRParameter) = length(p.beta_rest) + 1
struct CopyVector <: Kirstine.CovariateParameterization end
function Kirstine.map_to_covariate!(c::LLRCovariate, dp, m::LinLogReg, cp::CopyVector)
if length(dp) != length(c.x)
error("dimension of covariate and design point don't match")
end
c.x .= dp
return c
end
function nonlinear_predictor(m::LinLogReg, c::LLRCovariate, p::LLRParameter)
dim_c = length(c.x)
if length(p.beta_rest) != dim_c
error("dimensions of covariate and parameter don't match")
end
np = p.beta_0
for j in 1:dim_c
np += p.beta_rest[j] * c.x[j]
end
return np
end
function predictor_jacobianmatrix!(jm, m::LinLogReg, c::LLRCovariate, p::LLRParameter)
dim_c = length(c.x)
if length(p.beta_rest) != dim_c
error("dimensions of covariate and parameter don't match")
end
jm[1, 1] = 1
for j in 1:dim_c
jm[1, j + 1] = c.x[j]
end
return jm
end1-Dimensional Covariate
First, let's look at a locally optimal, 1-dimensional example from Section 6.2, p. 154 of [FL13], where
\[\begin{align*} \DesignRegion &= \CovariateSet = [0, 4] \\ \Parameter &= (-3, 1.81) \end{align*}\]
dp0 = DesignProblem(
criterion = DCriterion(),
region = DesignInterval(:x1 => (0, 4)),
covariate_parameterization = CopyVector(),
prior_knowledge = PriorSample([LLRParameter(-3, [1.81])]),
model = LinLogReg(1),
)
Random.seed!(12345)
str0 = DirectMaximization(
optimizer = Pso(swarmsize = 100, iterations = 50),
prototype = random_design(region(dp0), 4),
)
Random.seed!(12345)
s0, r0 = solve(dp0, str0; maxdist = 1e-3)
s0DesignMeasure(
[0.8047475621673699] => 0.49999389060536853,
[2.5101732141323296] => 0.5000061093946315,
)gd0 = plot_gateauxderivative(s0, dp0)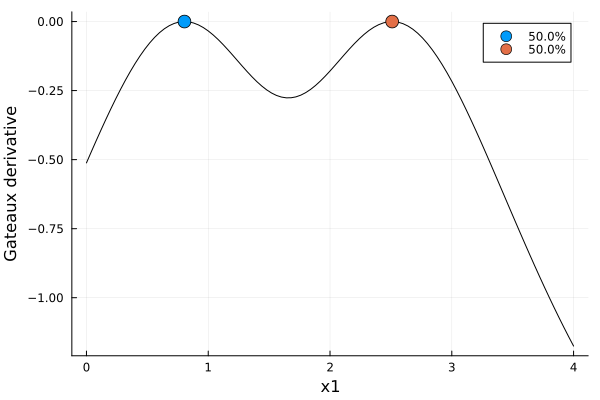
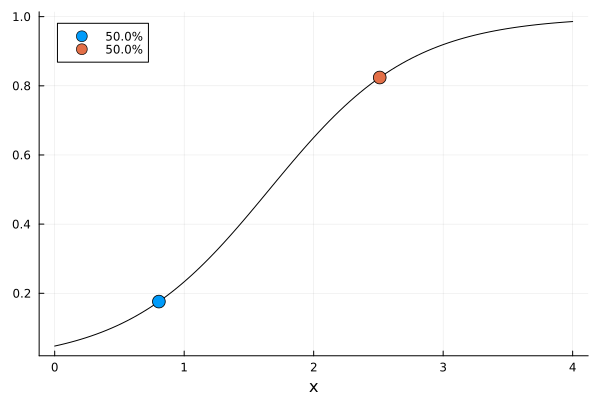
er0 = plot_expected_function(
(x, c, p) -> expit(p.beta_0 + p.beta_rest[1] * x),
c -> [c.x[1]],
(c, p) -> [expit(p.beta_0 + p.beta_rest[1] * c.x[1])],
range(lowerbound(region(dp0))[1], upperbound(region(dp0))[1]; length = 101),
s0,
model(dp0),
covariate_parameterization(dp0),
prior_knowledge(dp0);
xguide = "x",
)
2-Dimensional Covariate
Next, we are looking at a 2-dimensional design that is locally optimal for estimating the odds ratios
\[\Transformation(\Parameter) = (\exp(β₁), \exp(β₂))'.\]
when
\[\begin{align*} \DesignRegion &= \CovariateSet = [0, 1]^2 \\ \Parameter &= (-4, 6, -3) \end{align*}\]
dp1 = DesignProblem(
criterion = DCriterion(),
region = DesignInterval(:x1 => (0, 1), :x2 => (0, 1)),
covariate_parameterization = CopyVector(),
prior_knowledge = PriorSample([LLRParameter(-4, [6, -3])]),
model = LinLogReg(2),
transformation = DeltaMethod(p -> [0 exp(p.beta_rest[1]) 0; 0 0 exp(p.beta_rest[2])]),
)
Random.seed!(12345)
str1 = DirectMaximization(
optimizer = Pso(swarmsize = 100, iterations = 50),
prototype = random_design(region(dp1), 4),
)
Random.seed!(12345)
s1, r1 = solve(dp1, str1; maxdist = 5e-2, maxweight = 1e-3)
gd1 = plot_gateauxderivative(s1, dp1)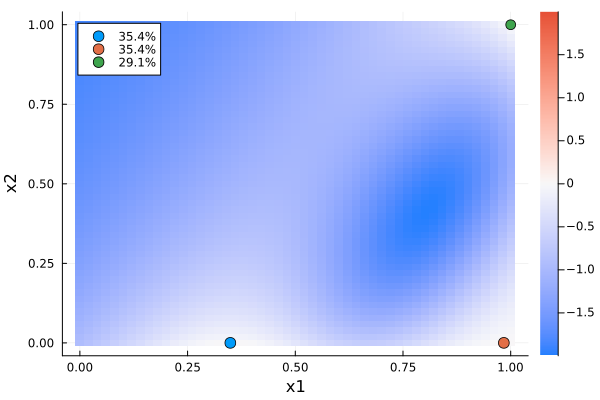
function erplot1(d, dp)
f1(x, c, p) = expit(p.beta_0 + p.beta_rest[1] * x + p.beta_rest[2] * c.x[2])
f2(x, c, p) = expit(p.beta_0 + p.beta_rest[1] * c.x[1] + p.beta_rest[2] * x)
g1(c) = [c.x[1]]
g2(c) = [c.x[2]]
h(c, p) = [expit(p.beta_0 + p.beta_rest[1] * c.x[1] + p.beta_rest[2] * c.x[2])]
xrange = range(lowerbound(region(dp))[1], upperbound(region(dp))[1]; length = 101)
cp = covariate_parameterization(dp)
pk = prior_knowledge(dp)
m = model(dp)
p1 = plot_expected_function(f1, g1, h, xrange, d, m, cp, pk; xguide = "x1")
p2 = plot_expected_function(f2, g2, h, xrange, d, m, cp, pk; xguide = "x2")
return plot(p1, p2)
end
er1 = erplot1(s1, dp1)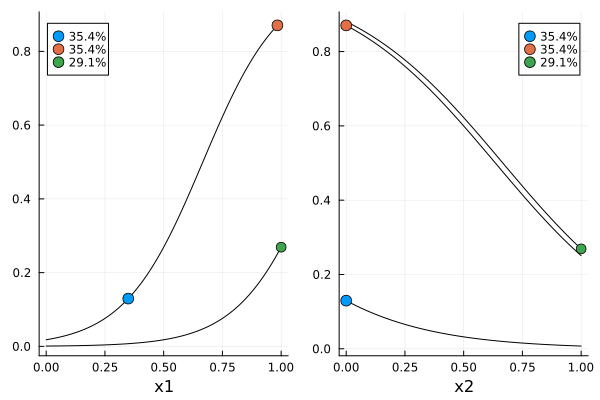
Nonlinear Predictor
A slightly silly example.
\[ν(\Covariate, \Parameter) = a \sin(2π b (t - c))\]
where $\Covariate = t$ and $\Parameter = (a, b, c)$ with $a > 0$, $b > 0$ and $0 ≤ c < 1$. We are interested in estimating all of $\Parameter$.
struct SinLogReg <: LogisticRegression end
mutable struct Time <: Kirstine.Covariate
t::Float64
end
Kirstine.allocate_covariate(m::SinLogReg) = Time(0)
@simple_parameter SLR a b c
function nonlinear_predictor(m::SinLogReg, c::Time, p::SLRParameter)
return p.a * sin(2 * pi * p.b * (c.t - p.c))
end
function predictor_jacobianmatrix!(jm, m::SinLogReg, c::Time, p::SLRParameter)
sin_term = sin(2 * pi * p.b * (c.t - p.c))
cos_term = cos(2 * pi * p.b * (c.t - p.c))
jm[1, 1] = sin_term
jm[1, 2] = p.a * cos_term * 2 * pi * (c.t - p.c)
jm[1, 3] = -p.a * cos_term * 2 * pi * p.b
return jm
end
function erplot2(d, dp)
f(x, c, p) = expit(p.a * sin(2 * pi * p.b * (x - p.c)))
g(c) = [c.t]
h(c, p) = [expit(p.a * sin(2 * pi * p.b * (c.t - p.c)))]
xrange = range(lowerbound(region(dp))[1], upperbound(region(dp))[1]; length = 101)
cp = covariate_parameterization(dp)
pk = prior_knowledge(dp)
m = model(dp)
return plot_expected_function(f, g, h, xrange, d, m, cp, pk; xguide = "time")
end
dp2 = DesignProblem(
criterion = DCriterion(),
region = DesignInterval(:t => (0, 1)),
covariate_parameterization = CopyTo(:t),
prior_knowledge = PriorSample([SLRParameter(a = 1, b = 1.5, c = 0.125)]),
model = SinLogReg(),
)
Random.seed!(12345)
str2 = DirectMaximization(
optimizer = Pso(swarmsize = 100, iterations = 50),
prototype = random_design(region(dp2), 4),
)
Random.seed!(12345)
s2, r2 = solve(dp2, str2; maxdist = 5e-2, maxweight = 1e-3)
gd2 = plot_gateauxderivative(s2, dp2)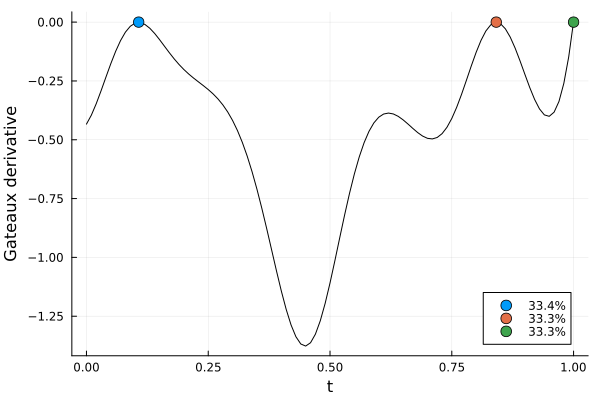
er2 = erplot2(s2, dp2)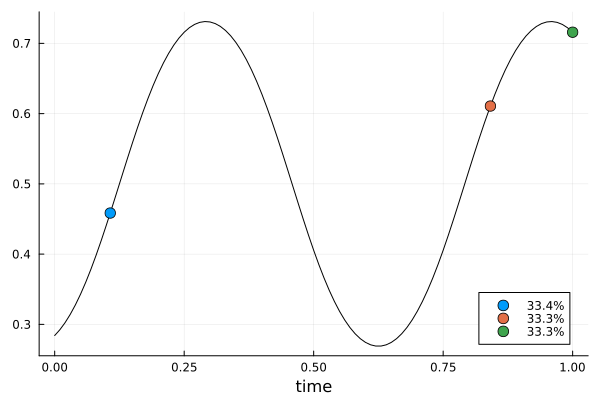
- FL13Valerii V. Fedorov and Sergei L. Leonov (2013). Optimal design for nonlinear response models. CRC Press. doi:10.1201/b15054