New Optimizer

Kirstine.jl comes with a simple particle swarm optimizer. This document describes how to implement a custom particle-based optimizer that seamlessly plugs into the rest of the package, such that it can be used with any Kirstine.ProblemSolvingStrategy.

Our example we will be a simplified version of the Imperialist-Competitive Algorithm (ICA) from the ICAOD R package. ICA is based on the following metaphor: a set of points represents countries, some of which are imperialists and some of which are colonies. An imperialist together with its associated colonies forms an empire. Initially, a given number of countries are designated as imperialists and colonies are assigned randomly. After that, the following steps are repeated:

• Assimilation: all colonies move a bit towards their imperialist.
• Revolution: some colonies move around randomly. The revolution rate decreases exponentially over time.
• Swap: a colony that has a better objective function value than its imperialist becomes the new imperialist of the empire.
• Unite: if the distance between two imperialists falls below a certain threshold, their empires are merged.
• Competition: in some iterations, stronger empires can try to steal a colony from the weakest empire. Strength of an empire is a weighted average of the objective functions values of its countries. If an empire has only zero or one colonies left, it is merged into the strongest empire.

Abstract Points

Before we get to the implementation details of ICA, we first need to understand how the optimization code in Kirstine.jl is structured. Particle-based optimizers typically expect to work with vectors from $\Reals^n$, as they need to perform the following operations on $x,y∈\Reals^n$ and $α∈\Reals$:

• $(x, y) ↦ x - y$: find the directional vector for moving from $y$ to $x$
• $(x, y) ↦ x + y$: update the position
• $(α, x) ↦ α x$: scale
• $(x, y) ↦ (x_1 y_1, …, x_n y_n)$: multiply element-wise

Of course, the set of DesignMeasures is not a vector space. But we can map a design measure

\[\DesignMeasure = \sum_{\IndexDesignPoint=1}^\NumDesignPoints \DesignWeight_{\IndexDesignPoint} \DiracDist(\DesignPoint_{\IndexDesignPoint})\]

on $\DesignRegion ⊂ \Reals^{\DimDesignRegion}$ to a vector in $\Reals^{\NumDesignPoints(\DimDesignRegion + 1) - 1}$ by

\[f(\DesignMeasure) = (\DesignPoint_1,…,\DesignPoint_{\NumDesignPoints}, \DesignWeight_1,…,\DesignWeight_{\NumDesignPoints-1})\]

and let the optimizer work on the representations $f(\DesignMeasure)$. Note that the final weight $\DesignWeight_{\NumDesignPoints}$ is not mapped, since it is implicitly known from the first $\NumDesignPoints - 1$ weights. A problem now is that in general there is no design measure

\[\text{“ } f^{-1}(f(\DesignMeasure_1) - f(\DesignMeasure_2)) \text{ ”}\]

since it could have negative weights or points outside $\DesignRegion$. Hence we need a different kind of object to represent these differences. For this, we used discrete signed measures. We denote the implied subtraction, addition, and multiplication operators by $⊖, ⊕, ⊙$. When adding a signed measure $\SignedMeasure$ to a design measure $\DesignMeasure$, we must take care that the weights and design points of the result $\DesignMeasure ⊕ \SignedMeasure$ are valid for a design measure.

Now, from a software engineering point of view, an Kirstine.Optimizer should not have to know anything about the nature of the points it works with. It only sees objects of a type T <: AbstractPoint, and a corresponding type U <: AbstractPointDifference that can store a representation of the difference between two Ts. This separates the optimization logic from the details of how the Ts should pretend to be vectors. The latter behavior is abstracted away into the following methods, shown here for T = DesignMeasure and U = SignedMeasure:

• ap_rand!(d::DesignMeasure, c::DesignConstraints): randomize d in place.
• ap_copy!(to::DesignMeasure, from::DesignMeasure): in-place assignment. Afterwards, to and from do not share memory.
• ap_diff!(v::SignedMeasure, p::DesignMeasure, q::DesignMeasure): compute $v = p ⊖ q$.
• ap_as_difference(p::DesignMeasure): return the SignedMeasure $v$ such that $f(v) = f(p)$.
• ap_rand!(v::SignedMeasure, lb::Real, ub::Real): randomize elements of v in place from a uniform distribution on the interval $[lb, ub]$.
• ap_mul!(v1::SignedMeasure, v2::SignedMeasure): in-place element-wise multiplication of v1 and v2.
• ap_mul!(v::SignedMeasure, a::Real): in-place multiplication of each element of v by a.
• ap_add!(v1::SignedMeasure, v2::SignedMeasure): update $v_1$ to $v_1 ⊕ v_2$.
• ap_add!(p::DesignMeasure, v::SignedMeasure, c::DesignConstraints): try to move from $p$ to $p ⊕ v$. If this would result in points outside the design region or invalid weights, move as far as possible in the direction of $v$.

Implementation

The internal optimization interface consists of functions that operate on objects of a type O <: Kirstine.Optimizer, which holds the algorithm's parameters, and a type S <: OptimizerState which holds the state of the optimizer in the current iteration. For O = Ica and S = IcaState we must implement the following methods:

• iterations(optimizer::Ica): accessor for the number of iterations that ICA should run
• maximizer(state::IcaState): accessor for the best candidate seen so far
• maximum(state::IcaState): accessor for the best objective value seen so far
• n_eval_f(state::IcaState): accessor for the cumulative number of evaluations of the objective function
• n_eval_g(state::IcaState): accessor for the cumulative number of evaluations of the gradient of the objective function (always 0 since ICA does not use gradients)
• optimizer_state(f, o::Ica, prototypes::Vector{AbstractPoint}, constraints::AbstractConstraints): constructor of an IcaState for the objective function f and parameters o. It should use the given prototypes for initialization and take the constraints into account for randomization. Setting up the state is counted as the first iteration of the algorithm.
• tick!(f, state::IcaState, optimizer::Ica, constraints::AbstractConstraints, iter::Integer): update the optimizers state once. This function is called internally iterations() - 1 times. The number of the current iteration is passed in iter, it goes from 2 to iterations().

using Kirstine
using Statistics: mean

struct Ica <: Kirstine.ZerothOrderOptimizer
    iterations::Int64
    num_countries::Int64
    num_initial_empires::Int64
    revolution_rate::Float64      # proportion of colonies where revolution happens
    damp::Float64                 # damping factor for revolution rate
    zeta::Float64                 # mean colony weight for power
    beta::Float64                 # assimilation speed
    competition_pressure::Float64 # probability that competition occurs
    uniting_threshold::Float64    # min relative distance for imperialists
    function Ica(i::Integer, nc::Integer, nie::Integer, rr, d, z, b, cp, ut)
        if i <= 0
            error("number of iterations must be positive")
        end
        if d <= 0 || d >= 1
            error("damping factor must be in (0, 1)")
        end
        if cp < 0 || cp > 1
            error("competition pressure must be in [0, 1]")
        end
        if rr < 0 || rr > 1
            error("revolution rate must be in [0, 1]")
        end
        if nie > nc ÷ 2
            error("at most half of the countries can be imperialists")
        end
        return new(i, nc, nie, rr, d, z, b, cp, ut)
    end
end

# keyword constructor
function Ica(;
    iterations,
    num_countries,
    num_initial_empires,
    revolution_rate,
    damp,
    zeta,
    beta,
    competition_pressure,
    uniting_threshold,
)
    return Ica(
        iterations,
        num_countries,
        num_initial_empires,
        revolution_rate,
        damp,
        zeta,
        beta,
        competition_pressure,
        uniting_threshold,
    )
end

Kirstine.iterations(optimizer::Ica) = optimizer.iterations

mutable struct IcaState{T,U} <: Kirstine.OptimizerState{T,U}
    country::Vector{T}            # all countries
    val::Vector{Float64}          # function values for all countries
    imperialist::Vector{Int64}    # contry index for each imperialist
    empire::Vector{Vector{Int64}} # country indices for colonies of each empire
    power::Vector{Float64}        # power of an of empire
    rand::U                       # tmp for uniform random number for assimilation update
    diff::U                       # tmp for difference imperialist - colony
    revolution_rate::Float64      # current revolution rate
    n_eval::Int64                 # cumulative number of objective evaluations
end

Kirstine.maximizer(state::IcaState) = state.country[argmax(state.val[state.imperialist])]
Kirstine.maximum(state::IcaState) = maximum(state.val[state.imperialist])
Kirstine.n_eval_f(state::IcaState) = state.n_eval
Kirstine.n_eval_g(state::IcaState) = 0

function Kirstine.optimizer_state(
    f,
    o::Ica,
    prototypes::AbstractVector{<:Kirstine.AbstractPoint},
    constraints::Kirstine.AbstractConstraints,
)
    # initialize countries at prototypes, randomize the rest
    if o.num_countries < length(prototypes)
        error("num_countries must be at least as large as number of prototype particles")
    end
    cnt_given = deepcopy(prototypes)
    n_random = o.num_countries - length(prototypes)
    cnt_random = [deepcopy(prototypes[1]) for _ in 1:n_random]
    for k in 1:n_random
        Kirstine.ap_rand!(cnt_random[k], constraints)
    end
    country = [cnt_given; cnt_random]
    # get the matching difference type for the concrete type of country[1]
    zero_diff = Kirstine.ap_as_difference(country[1])
    Kirstine.ap_diff!(zero_diff, country[1], country[1]) # initialize at 0
    # allocate vectors for the state object
    val = fill(NaN, o.num_countries)
    imp = fill(0, o.num_initial_empires)
    emp = [[0] for _ in 1:(o.num_initial_empires)] # arbitrary invalid index
    tc = fill(NaN, o.num_initial_empires)
    rnd = deepcopy(zero_diff)
    diff = deepcopy(zero_diff)
    # instantiate a state object and initialize it properly
    state = IcaState(country, val, imp, emp, tc, rnd, diff, o.revolution_rate, 0)
    ica_evaluate_objective!(f, state)
    num_colonies = o.num_countries - o.num_initial_empires
    state.imperialist .= sortperm(state.val, rev = true)[1:(o.num_initial_empires)]
    # there is at least one country per empire, with additional ones depending on power
    empsize = fill(1, o.num_initial_empires)
    min_val = minimum(state.val[state.imperialist])
    imperialist_power = (0.3 * sign(min_val) - 1) .* min_val .+ state.val[state.imperialist]
    imperialist_power ./= sum(imperialist_power)
    # we use the apportionment procedure to make sure empire sizes add up
    empsize .+= apportion(imperialist_power, num_colonies - o.num_initial_empires)
    # partition the remaining countries according to empire sizes
    colony_indices = setdiff(1:(o.num_countries), state.imperialist)
    for k in 1:(o.num_initial_empires)
        # consume colony index list in empsize-sized chunks
        state.empire[k] = colony_indices[1:empsize[k]]
        colony_indices = colony_indices[(empsize[k] + 1):end]
    end
    ica_compute_power!(state, o)
    @debug "INIT" state.empire
    return state
end

function Kirstine.tick!(
    f,
    state::IcaState,
    optimizer::Ica,
    constraints::Kirstine.AbstractConstraints,
    iter::Integer,
)
    @debug "Iteration $iter"
    ica_assimilate!(state, optimizer, constraints)
    ica_revolt!(state, optimizer, constraints)
    ica_evaluate_objective!(f, state)
    ica_swap!(state)
    ica_unite!(state, optimizer)
    ica_compute_power!(state, optimizer)
    ica_compete!(state, optimizer)
end

# For each empire k and colony j,
# move col_{k,j} → col_{k,j} + r .* (imp_{k} - col_{k,j})
# where r is a vector of uniform random numbers on [0, β].
function ica_assimilate!(
    state::IcaState,
    optimizer::Ica,
    constraints::Kirstine.AbstractConstraints,
)
    for k in 1:length(state.empire)
        imp = state.imperialist[k]
        for j in 1:length(state.empire[k])
            col = state.empire[k][j]
            Kirstine.ap_rand!(state.rand, 0, optimizer.beta)
            Kirstine.ap_diff!(state.diff, state.country[imp], state.country[col])
            Kirstine.ap_mul!(state.diff, state.rand)
            Kirstine.ap_add!(state.country[col], state.diff, constraints)
        end
    end
    return state
end

# For each empire, move a proportion of colonies around randomly. The proportion equals the
# current revolution rate. The maximal distance is four times the distance between colony
# and imperialist.
# A colony col_{k,j} where a revolution happens is moved to
# col_{k,j} + β .* r .* (imp_{k} - col_{k,j})
# where r is a vector of uniform random numbers on [-β/2, β/2]
# I.e. the difference to assimilation is that only some colonies are affected,
# and that they can also move _away_ from their imperialist.
function ica_revolt!(
    state::IcaState,
    optimizer::Ica,
    constraints::Kirstine.AbstractConstraints,
)
    state.revolution_rate *= optimizer.damp
    for k in 1:length(state.empire)
        num_col = length(state.empire[k])
        num_rev = Int64.(floor(state.revolution_rate * num_col))
        imp = state.imperialist[k]
        if num_rev > 0
            rev_idx = randperm(num_col)[1:num_rev]
            for j in rev_idx
                col = state.empire[k][j]
                dist = Kirstine.ap_dist(state.country[imp], state.country[col])
                Kirstine.ap_rand!(state.rand, -optimizer.beta / 2, optimizer.beta / 2)
                Kirstine.ap_add!(state.country[col], state.diff, constraints)
            end
        end
    end
    return state
end

function ica_evaluate_objective!(f, state::IcaState)
    for i in 1:length(state.country)
        state.val[i] = f(state.country[i])
    end
    state.n_eval += length(state.country)
    return state
end

# iterate through empires and swap colony with imperialist if the colony has a better objective value
function ica_swap!(state::IcaState)
    for k in 1:length(state.empire)
        for j in 1:length(state.empire[k])
            country_imp = state.imperialist[k]
            country_col = state.empire[k][j]
            val_imp = state.val[country_imp]
            val_col = state.val[country_col]
            if val_col > val_imp
                @debug "SWAP colony $j (country $country_col) with imperialist $k (country $country_imp)"
                state.imperialist[k] = country_col
                state.empire[k][j] = country_imp
            end
        end
    end
    return state
end

# loop through pairs of empires and merge any where the imperialists are less than `uniting_threshold` apart
function ica_unite!(state::IcaState, optimizer::Ica)
    k = 1
    while k < length(state.empire) # note: the length can change in the loop body
        l = k + 1
        while l <= length(state.empire)
            imp_k = state.imperialist[k]
            imp_l = state.imperialist[l]
            if Kirstine.ap_dist(state.country[imp_k], state.country[imp_l]) <=
               optimizer.uniting_threshold
                idx_src, idx_dst = state.val[imp_k] > state.val[imp_l] ? (l, k) : (k, l)
                @debug "UNITE empire $idx_src with empire $idx_dst"
                append!(state.empire[idx_dst], state.empire[idx_src])
                push!(state.empire[idx_dst], state.imperialist[idx_src])
                deleteat!(state.empire, idx_src)
                deleteat!(state.power, idx_src)
                deleteat!(state.imperialist, idx_src)
            end
            l += 1
        end
        k += 1
    end
    return state
end

# an empires power is the weighted mean of the objective functions's values at its
# imperialist and its colonies, shifted such that the minimum is zero
function ica_compute_power!(state::IcaState, optimizer::Ica)
    for k in 1:length(state.empire)
        state.power[k] =
            state.val[state.imperialist[k]] +
            optimizer.zeta * mean(state.val[state.empire[k]])
    end
    idx_finite = .!isinf.(state.power)
    state.power .-= minimum(state.power[idx_finite]) # prevent subtracting -Inf
    state.power[.!idx_finite] .= 0
    return state
end

function ica_compete!(state::IcaState, optimizer::Ica)
    if length(state.empire) == 1 ||
       all(==(0), state.power) ||
       rand() > optimizer.competition_pressure
        return state
    end
    idx_src = argmin(state.power)
    # sample empire index with given probabilities
    idx_dst = findfirst(cumsum(state.power) .> rand() * sum(state.power))
    # sample colony index uniformly
    idx_col = rand(1:length(state.empire[idx_src]))
    @debug "MOVE colony $(idx_col) (country $(state.empire[idx_src][idx_col])) from empire $(idx_src) to empire $(idx_dst)"
    # move selected colony to destination empire
    push!(state.empire[idx_dst], state.empire[idx_src][idx_col])
    deleteat!(state.empire[idx_src], idx_col)
    # merge source empire with strongest if only one colony remaining
    if length(state.empire[idx_src]) <= 1 # can be 0 if an empire was initialized with just 1 colony
        @debug "DELETE empire $(idx_src)"
        # move last remaining colony to strongest empire
        if length(state.empire[idx_src]) == 1
            push!(state.empire[idx_dst], state.empire[idx_src][1])
        end
        # move former imperialist to strongest empire
        push!(state.empire[idx_dst], state.imperialist[idx_src])
        # delete the former empire and imperialist and its power
        deleteat!(state.empire, idx_src)
        deleteat!(state.imperialist, idx_src)
        deleteat!(state.power, idx_src)
    end
    return state
end

Notable differences to the ICA implementation in the ICAOD package are:

• no local search phase
• Monte-Carlo integration instead of HCubature
• uniting_threshold is an absolute quantity
• collisions with the boundary are handled differently

Example

For illustration, we re-use the example with the discrete prior.

using Kirstine, Random, Plots

@simple_model SigEmax dose
@simple_parameter SigEmax e0 emax ed50 h

function Kirstine.jacobianmatrix!(
    jm,
    m::SigEmaxModel,
    c::SigEmaxCovariate,
    p::SigEmaxParameter,
)
    dose_pow_h = c.dose^p.h
    ed50_pow_h = p.ed50^p.h
    A = dose_pow_h / (dose_pow_h + ed50_pow_h)
    B = ed50_pow_h * p.emax / (dose_pow_h + ed50_pow_h)
    jm[1, 1] = 1.0
    jm[1, 2] = A
    jm[1, 3] = -A * B * p.h / p.ed50
    jm[1, 4] = c.dose == 0 ? 0.0 : A * B * log(c.dose / p.ed50)
    return jm
end

prior = PriorSample(
    [SigEmaxParameter(e0 = 1, emax = 2, ed50 = 0.4, h = h) for h in 1:4],
    [0.1, 0.3, 0.4, 0.2],
)

dp = DesignProblem(
    criterion = DCriterion(),
    region = DesignInterval(:dose => (0, 1)),
    model = SigEmaxModel(sigma = 1),
    covariate_parameterization = JustCopy(:dose),
    prior_knowledge = prior,
)

strategy = DirectMaximization(
    optimizer = Ica(
        iterations = 100,
        num_countries = 100,
        num_initial_empires = 20,
        # settings (mostly) as in ICAOD defaults
        revolution_rate = 0.3,
        damp = 0.99,
        zeta = 0.1,
        beta = 4,
        competition_pressure = 0.11,
        uniting_threshold = 1.0,
    ),
    prototype = equidistant_design(region(dp), 8),
)

Random.seed!(31415)
s, r = solve(dp, strategy, maxweight = 1e-3, maxdist = 1e-2, trace_state = true)
gd = plot_gateauxderivative(s, dp)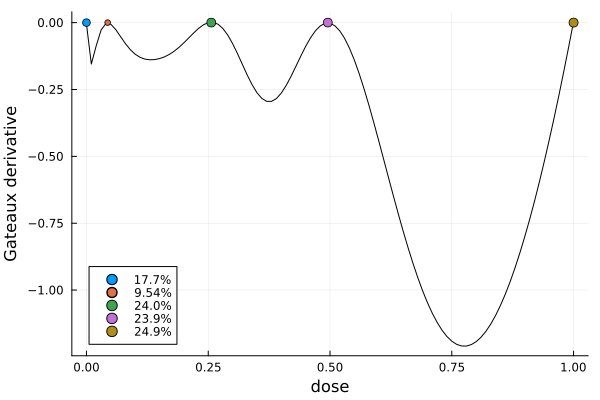

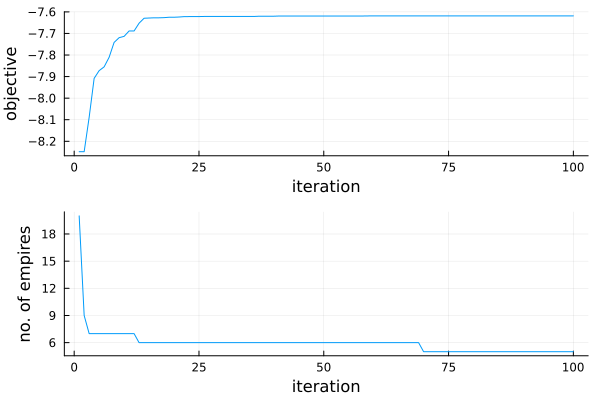
n_emp = map(st -> length(st.empire), optimization_result(r).trace_state)
dia = plot(
    plot(r),
    plot(n_emp; xguide = "iteration", yguide = "no. of empires", legend = nothing),
    layout = (2, 1),
)