New Problem Solving Strategy
On a high level, Kirstine.jl can use different Kirstine.ProblemSolvingStrategys to find the solution to a design problem. The package implements DirectMaximization and a version of Fedorov's Exchange algorithm. This vignette shows how to implement a custom strategy.
Our example will be a variant of direct maximization that runs the given Kirstine.Optimizer multiple times, using the best candidate from the current iteration as the prototype for initializing the next one. A further extension of this example could also include a check of the Gateaux derivative for early stopping.
Implementation
For a Ts <: Kirstine.ProblemSolvingStrategy we need a corresponding Tr <: Kirstine.ProblemSolvingResult, plus methods for the following functions:
solve_with(adp::AbstractDesignProblem, strategy::Ts, trace_state::Bool)which does the actual work and returns aTr. The flagtrace_stateshould passed to the low-levelKirstine.Optimizer.solution(res::Tr)to extract the best solution that was found.total_runtime(res::Tr)to extract the total runtime in seconds.
Optionally, for producing a plot of the optimization progress, we can also implement a type recipe for Tr. When it comes to plotting a Vector of Kirstine.OptimizationResults, Kirstine.jl already provides a basic recipe that we can reuse.
For simplicity we require the low-level optimizer to be of order zero.
using Kirstine, RecipesBase, Plots
struct MultipleRuns{T<:Kirstine.ZerothOrderOptimizer} <: Kirstine.ProblemSolvingStrategy
optimizer::T
prototype::DesignMeasure
steps::Int64
fixedweights::Vector{Int64}
fixedpoints::Vector{Int64}
function MultipleRuns(;
optimizer::T,
prototype::DesignMeasure,
steps::Integer,
fixedweights::AbstractVector{<:Integer} = Int64[],
fixedpoints::AbstractVector{<:Integer} = Int64[],
) where T<:Kirstine.ZerothOrderOptimizer
new{T}(optimizer, prototype, steps, fixedweights, fixedpoints)
end
end
struct MultipleRunsResult{
S<:Kirstine.OptimizerState{DesignMeasure,Kirstine.SignedMeasure},
} <: Kirstine.ProblemSolvingResult
ors::Vector{Kirstine.OptimizationResult{DesignMeasure,Kirstine.SignedMeasure,S}}
end
function Kirstine.solution(mrr::MultipleRunsResult)
return mrr.ors[end].maximizer
end
function Kirstine.total_runtime(mrr::MultipleRunsResult)
return mapreduce(or -> or.seconds_elapsed, +, mrr.ors)
end
function Kirstine.solve_with(
adp::Kirstine.AbstractDesignProblem,
strategy::MultipleRuns,
trace_state::Bool,
)
# `Kirstine.optimize()` needs to know the constraints for the optimization problem.
constraints = Kirstine.DesignConstraints(
strategy.prototype,
region(adp),
strategy.fixedweights,
strategy.fixedpoints,
)
# set up preallocated objects for the objective function to work on
oc = Kirstine.objective_constants(adp)
w = Kirstine.allocate_workspace(strategy.prototype, adp)
optimization_helper(prototype) = Kirstine.optimize(
d -> Kirstine.objective!(w, d, adp, oc),
strategy.optimizer,
[prototype],
constraints;
trace_state = trace_state,
)
# initial run
ors = [optimization_helper(strategy.prototype)]
# subsequent runs
for i in 2:(strategy.steps)
new_prototype = ors[i - 1].maximizer
or = optimization_helper(new_prototype)
push!(ors, or)
end
return MultipleRunsResult(ors)
end
@recipe function f(r::MultipleRunsResult)
return r.ors # just need to unwrap
endExample
Again, we use the discrete prior example.
using Kirstine, Random, Plots
@simple_model SigEmax dose
@simple_parameter SigEmax e0 emax ed50 h
function Kirstine.jacobianmatrix!(
jm,
m::SigEmaxModel,
c::SigEmaxCovariate,
p::SigEmaxParameter,
)
dose_pow_h = c.dose^p.h
ed50_pow_h = p.ed50^p.h
A = dose_pow_h / (dose_pow_h + ed50_pow_h)
B = ed50_pow_h * p.emax / (dose_pow_h + ed50_pow_h)
jm[1, 1] = 1.0
jm[1, 2] = A
jm[1, 3] = -A * B * p.h / p.ed50
jm[1, 4] = c.dose == 0 ? 0.0 : A * B * log(c.dose / p.ed50)
return jm
end
prior = PriorSample(
[SigEmaxParameter(e0 = 1, emax = 2, ed50 = 0.4, h = h) for h in 1:4],
[0.1, 0.3, 0.4, 0.2],
)
dp = DesignProblem(
criterion = DCriterion(),
region = DesignInterval(:dose => (0, 1)),
model = SigEmaxModel(sigma = 1),
covariate_parameterization = CopyTo(:dose),
prior_knowledge = prior,
)
strategy = MultipleRuns(
optimizer = Pso(iterations = 20, swarmsize = 25),
prototype = equidistant_design(region(dp), 8),
steps = 10,
)
Random.seed!(31415)
s, r = solve(dp, strategy, maxweight = 1e-3, maxdist = 1e-2)
gd = plot_gateauxderivative(s, dp)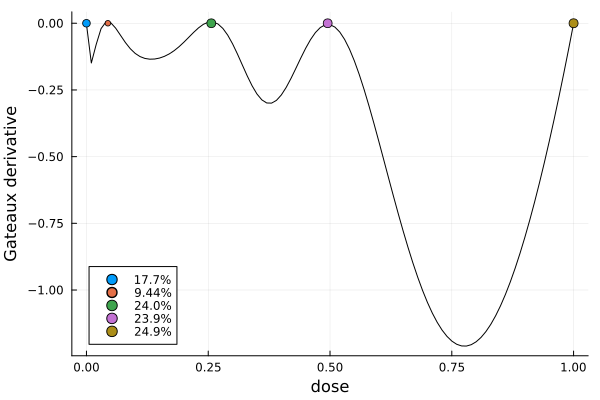
total_runtime(r)0.07813906669616699pr = plot(r)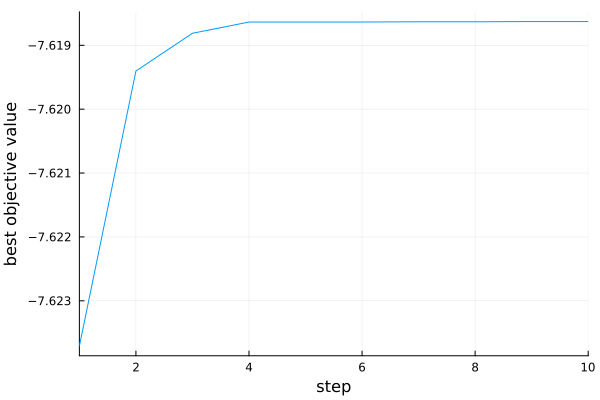
We see that the solution was found after four steps.